Behavior of Square Roots When x is between 0 and 1

Small numbers between 0-1 has always stumped me as it’s behaviors seemed unintuitive. For instance:

• $0.5^2 = 0.5 \cdot 0.5 = 0.25$
• $\sqrt{0.5} \approx 0.707106781$

which implies for $x \in (0,1)$:

• $x^2 \lt x$
• $\sqrt{x} \gt x$

I can rationalize in my head the first example by transforming the problem $x^2$ from an abstract equation into a more concrete word problem:

What is half of a half

Half is 50% and a half of 50% is 25%. While suffice enough to convince my brain, this lacks sufficient rigor in Mathematics. So let’s go through the proof a bit more formally as to why $x^2 \lt x$ because we’ll need this premise to explain why $x \lt \sqrt{x}$ for $x\in \{0,1\}$:

\[\begin{align*} 0 &\lt x \lt 1 \\ x\cdot 0 &\lt x\cdot x \lt 1\cdot x \\ 0 &\lt x^2 \lt x \end{align*}\]

There are two ways I can think when it comes to explaining why $x \lt \sqrt{x}$:

1. Graphically:

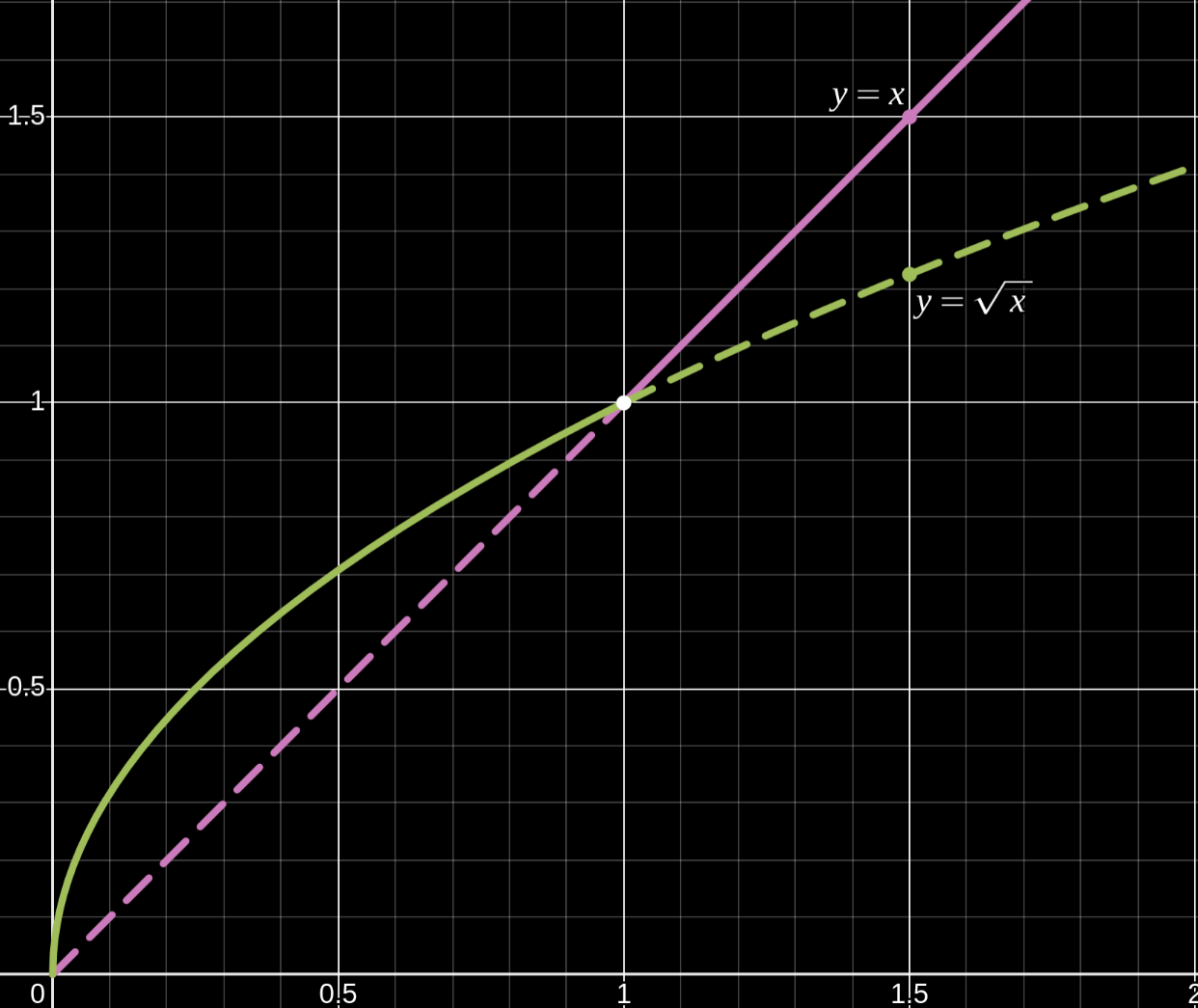
Observe how the root function $\sqrt{x}$ domaintes the linear function $x$ for $x\in (0, 1)$ i.e. $x \lt \sqrt{x}, \forall x \in (0,1)$

2. Formal Proofs:

\[\begin{align*} 0 &\lt x \lt 1 \\ 0\cdot x &\lt x \cdot x \lt 1 \cdot x \\ 0 &\lt x^2 \lt x \\ \sqrt{0} &\lt \sqrt{x^2} \lt \sqrt{x} \\ 0 &\lt |x| \lt \sqrt{x} \quad x \gt 0 \\ 0 &\lt x \lt \sqrt{x} \\ & \boxed{x \lt \sqrt{x} \quad \forall x \in (0,1)} \end{align*}\]

or given $x^2 \lt x \quad \forall x \in (0,1)$ as shown in the beginning:

\[\begin{align*} x^2 &\lt x \\ \sqrt{x^2} &\lt \sqrt{x} \\ |x| &\lt \sqrt{x} \\ &\boxed{x \lt \sqrt{x} \quad \forall x \in (0,1)} \end{align*}\]