MATH2107 - Linear Algebra II
August 25, 2022
This is a course review of MATH2107 - Linear Algebra II taken at CarletonU in the summer of 2022. The course took a “reverse-style” classroom teaching where the lectures were pre-recorded and students were expected (but was optional) to attend lectures to solve problems relating to the lectures. The tutorials were also in-person. The review will be split into two main sections, a long commentary about what the course is about and a section dedicated to reviewing and discussing the organization of the course and how I studied for the course.
last major edit: 2022-11-29
TLDR:
- Less theoretical compared to MATH2152 that I was supposed to take
- Kyle Harvey is a very good instructor, you should take it with him if you can. In fact, he is THE instructor to learn Linear Algebra from
- Very clear and concise lecture slides
- Attend lectures that are optional for the bonus marks and to get more practice
- A good number of topics overlap with MATH1104 but this course goes more in-depth
- Know how to row-reduce or learn how early in the course

Taken from the Manga Guide to Linear Algebra
Professor: Kyle Harvey
Course Delivery: “Reverse-style” Classroom where lectures are pre-recorded, the in-person lectures and tutorials go over problems (except lecture problems give you possible bonus points)
Class Size: About 40 students
Course Description (from website): Finite-dimensional vector spaces (over R and C), subspaces, linear independence and bases. Linear transformations and matrices. Inner product spaces (over R and C); Orthonormal bases. Eigenvalues and diagonalization. Bilinear and quadratic forms; principal axis theorem.
Course Description (LONG) with Commentary:
| Week | Topic |
|---|---|
| Week 1 | Vector Spaces, Subspaces, Linear Combinations and Span |
| Week 2 | Linear Independence, Basis, Colspace, Rowspace, Nullspace, Rank Nullity THM |
| Week 3 | Coordinate Vectors, Change of Basis Matrix |
| Week 4 | Eigenvalues and Eigvenvectors |
| Week 5 | Eigenspaces, Geometric Multiplicity, diagonalization, and fast matrix multiplication |
| Week 6 | Linear Transformations, Kernel, and Range for Transformations |
| Week 7 | Matrix Representation of Transformations, Injective, Surjective, and Bijective Transformations |
| Week 8 | Dot Products, Norm, Distance, Unit Vectors, Oethogonal sets, orthogonal basis, orthogonal complement, and orthogonal matrices |
| Week 9 | Orthogonal Projections and Decompositions, Gram Schmidt, and QR Factorization |
| Week 10 | Least Squares Method, Inner Products |
| Week 11 | Orthogonal Basis, Projections and Decompositions for Inner Products |
| Week 12 | Diagonalization of Symmetric Matrices, Spectral Theorem, Quadratic Forms, and Principle Axis Theorem |
Oddly enough, MATH2107 begins with working on proofs for a course that does not have an emphasis on proofs. It reminds me of how MATH1052 (Calc 1 Honors) and MATH1152 (Linear Algebra I Honors) began with proofs involving some field. The course begins by talking about vector spaces, what they are, and their properties. This is probably annoying for many students who are not comfortable with proofs. It is not that proving vector spaces are difficult, it’s just tedious. The proof is just equating the left side and the right side of a given property. The course does not expect students to prove all 8 properties that define a vector space. A typical proof question involving a vector space is to either find a counter-example to the claim or to provide a Left Side = Right Side proof of a given property. Naturally, the topic of vector spaces transitioned to discussing what a subspace is and how to prove a set is a subspace of a known vector space. Those who have done MATH1152 (Linear Algebra I Honors) would probably have been familiar with the topic of vector space and subspace already. A new vector space he introduces is the Polynomial space which is something I did not see before. A polynomial vector space is simply just polynomials with coefficients in some field such as $\mathbb{R}$ but it was interesting to see a space I did not recognize. After this topic, students will go back to familiar territory talking about linear combinations and span. Although I am not familiar with what MATH1104 and MATH1107 cover but the next few topics should be review such as the idea of linear independence, basis, dimensions, colspace, rowspace, nullspace, and the rank-nullity theorem.
The course then progress to talk about coordinate vectors and change of basis matrix. Coordinate vectors are essentially a way to represent uniquely a vector as a linear combination of vectors belonging to some basis by storing the coefficient as a $\mathbb{R}^n$ or $\mathbb{C}^n$ vector. Although it is not an entirely interesting idea, being able to store coefficients into a vector, is a very powerful tool that you may be using without realizing. One often usage of coordinate vectors is when trying to find a linear combination of a vector given some basis or check which vectors in the set are linearly independent. A quick shortcut to form the augmented matrix is to set the columns of the matrix as the coordinate vectors of each coordinate in respect to the standard basis.
\[\begin{align*} S= \{ \begin{bmatrix} 1 & -1 \\ 0 & 1 \\ \end{bmatrix}, \begin{bmatrix} 4 & 3 \\ 2 & 1 \\ \end{bmatrix}, \begin{bmatrix} 7 & 7 \\ 4 & 1 \\ \end{bmatrix}, \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix} \} \end{align*}\]An illustration of how coordinate vectors can be useful.
Although it is intuitive how to represent any vector using the standard basis, it’s not the only way to compose any vector. Recall how a linear combination is simply decomposing a given vector into a sum of the vectors in the basis (i.e. $v = c_1 v_1 + c_2 v_2 + … + c_n v_n$). What happens if you want to represent the vector with respect to a different base. So far, we have only been dealing with a single basis but we can introduce another basis to the problem. Although not apparent as to why we would do this, it will make more sense when we deal with transformation matrices later in the course. Linear Algebra or math in general (but more so in linear algebra) is a series of steps where topics are introduced in bite-size chunks so that you can solve more complex problems in the future. So it is very important that you understand the fundamentals and the previous topics in this course or else you will quickly get lost in the course (i.e. you cannot play soccer if you don’t know how to walk first). A change of basis matrix is a matrix representation between two different bases and is often represented as P or $P_{C\leftarrow B}$. I prefer adding the subscript to the change of basis matrix because it helps me visualize both the problem and its solution. It makes it simple to remember how to convert a vector from one basis to another.
\[\begin{align*}[x]_C = P_{C\leftarrow B} [x]_B\end{align*}\]Converting a vector from the basis B to basis C. Note: This only provides the coordinate vector in respect to basis C and is not the vector itself.
One feature of the change of basis I found very cool is that you are able to extract the basis B from $P_{C\leftarrow B}$ given the basis C if the basis B is unknown. I do not know why I find this very fascinating but it reminds me of bit parity or a very stretched form of compacting data to reduce space (at the expense of speed since you need to calculate B from $P_{C\leftarrow B}$). This is due to the definition of the change of basis being:
\[\begin{align*} P_{C\leftarrow B} = \begin{bmatrix} [b_1]_{C} & [b_2]_{C} & ... & [b_n]_{C} \\ \end{bmatrix} \end{align*}\]This means that the first vector in the basis is a linear combination of vectors in C with the coefficients being the entries along the first column in the change of basis matrix. This is one way to verify if you determined the change of basis correctly but that’s only if you have time. Let’s avoid going down a rabbit hole on my fascination of change of basis and coordinate vectors and go onto the next topic that was taught in the course.

The next topic covered is eigenvector and eigenvalues which should look familiar from the previous course. Revisiting this topic 6 years later made me realize how beautiful the expression $Av = \lambda v$ is because of the few facts I took for granted and did not realize till watching Kyle’s lectures. The first property is that eigenvalues and eigenvectors are for SQUARE matrices. But that should have been obvious anyways (I was a brainless student back in the days). The neat feature of the equation is that if you know the eigenvalue $\lambda$, you can compute the result of Ax faster with the eigenvector v. Having done a lot of matrix multiplication, I really appreciate a faster approach and it goes back to my fascination with shortcuts that are either faster or smaller in data representation. The course goes through neat properties of diagonal, upper/lower triangles (a square matrix where the entries along the diagonal and upper/lower half can be any value and the opposite half have all their entries set to 0) and their eigenvalues (and eigenvectors if it is a diagonal matrix). One neat property I never knew about eigenvectors is that two eigenvectors belonging to two different eigenvalues are linearly independent of each other. Another topic covered was finding the determinants which may also be review. The course covers finding the determinants of 2x2, 3x3, and 4x4 matrices which are all review to me (the MATH1104 equivalent course I took covered this so I assume it’s the same at CarletonU). The reason why determinants are covered (aside from being able to figure out if a matrix has an inverse or not) is to determine all the eigenvalues for a particular square matrix through the characteristic equation.
\[\begin{align*} det(A-I\lambda) = 0 \end{align*}\]The characteristic equation to find all the eigenvalues
Something neat I learned from the course is that:
\[\begin{align*} Ax &= \lambda x \\ Ax - \lambda x &= 0 \\ x(A - \lambda) &= 0 \\ A - I \lambda &= 0 & \text{for v $\ne$ 0} \end{align*}\]You may or may not be wondering what is the significance of this aside from looking eerily similar to the characteristic equation. It turns out that to find the eigenvectors for each eigenvalue, it’s simply the $nul(A - I \lambda)$ meaning the product of between $(A - I \lambda)$ with a vector belonging to the eigenspace that you have found is equal to 0. This is one way to confirm if your answer is correct. This applies anytime you find vectors for the nullspace (i.e. by definition the nullspace of A is the set of vectors such that Ax = 0). A neat feature of eigenbasis is that the number of vectors in each of the eigenbasis cannot exceed the algebraic multiplicity of the eigenvalue. Recall that when determining the eigenvalue of a matrix, you factor the equation to find the solutions/roots to the equation. The number of times the particular solution solves the equation is the algebraic multiplicity of the eigenvalue. For instance,
\[\begin{align*}det(A - I\lambda) = (x)(x)(x-1)\end{align*}\]The equation has the roots: 0 and 1 but 0 solves the equation twice and therefore the algebraic multiplicity of 0 is 2. Knowing that the geomultiplicity (the number of vectors in the eigenbasis for a particular eigenvalue) cannot exceed the algebraic multiplicity can be an indicator if you are on the wrong track if you for instance found that you have more vectors than the algebraic multiplicity. However, this does not restrict the geomultiplicity from being smaller than the algebraic multiplicity.
The topic of geomultiplicity nicely transitions to the talk about whether a matrix is diagonalizable or not. While I do not have a good grasp what that means (hopefully once I finish reviewing MATH2152 materials before the school semester starts I would know), one property of diagonalizable matrix makes finding the product of the matrix multiplied by itself r times (i.e. $A^{80}$) in an efficient manner both in time and space complexity. A diagonalizable matrix is a matrix that can be represented as
\[\begin{align*}A = PDP^{-1}\end{align*}\]where P is any invertible matrix (in our case it’s the eigenbases as columns) and D is a diagonal matrix (which in our case would be the corresponding eigenvalues down the diagonal). So if you want to compute $A^{80}$, it’s simply just computing:
\[\begin{align*} A^{80} &= PD^{80}P^{-1} \\ &= P \begin{bmatrix} \lambda_1^{80} & 0 & 0 & ... & 0 \\ 0 & \lambda_2^{80} & 0 & ... & 0 \\ 0 & 0 & ... & 0 & 0 \\ & & ... \\ 0 & 0 & ... & 0 & \lambda_n^{80} \\ \end{bmatrix} P^{-1} \end{align*}\]The reason why I said geomultiplicities is a smooth transition to talking about diagonalization is that a matrix is only diagonalizable if the sum of geomultiplicities of all eigenspaces of the matrix sums to the size of the square matrix. A common theme I want to repeat is how every topic you learn in this course repeats so it is very crucial you understand the previous materials. If you were to construct a web mind of all the topics in this course, you probably get a very connected web/graph. I am very lazy to write one myself but you can check out this site that has a few mindmaps for linear algebra that I found while writing this review (this is only one of three mindmaps they have).

A sample mindmap of linear algebra and this is only one of three mindmaps from minireference.com
When working with finding the eigenvalues and eigenvectors, do look at the matrix before applying the characteristic equation because if the matrix is triangular or diagonal, the eigenvalue should be obvious without doing any extra work. The eigenvalues of a diagonal and upper triangular matrices are the diagonal entries of the matrix. For the diagonal matrix, the eigenvectors correspond to the standard basis where the ith eigenvalue corresponds to the ith vector in the standard basis. However, more work is required to find the eigenvector for upper triangular unfortunately but at least you do not need to find the eigenvalues.
On a side note, recall learning about complex numbers in the previous course? Being able to manipulate complex numbers comes in very handy as they appear in the course. They first appear when dealing with eigenvalues and eigenvectors as real matrices can have complex eigenvalues despite the matrix having all their entries being real. Row reducing complex matrices is a huge pain. The easiest method of dealing with row-reducing complex matrices is to multiply the column you are working with by its conjugate. You will see when you take the course and Kyle has a very good slide explaining how to reduce matrices (and actually everything taught in the course is all in his lecture notes in a very organized and clear fashion). Knowing how to work with complex numbers will also come in handy near the end of the course where inner products are covered.
The course introduces Linear Transformations that you probably vaguely remember from the previous course. I think of it as a function with a fancy name. This unit again involves another left side and right side proof to prove some transformation is linear or not. An interesting property of linear transformations is that if $T(v_1), T(v_2), …, T(v_n)$ are linearly independent then $v_1, v_2, …, v_n$ are linearly independent as well. This means that if you are not given the linear transformation but you have the output/result of the transformation for each basic vector, then you can determine what the output is for any vector in the basis. Perhaps I am exaggerating how fascinating this is, but the ability to obtain the output of a linear transformation without knowing the transformation is neat. In other words, you can know the output of any value from a function knowing some output of the basic essential inputs. As you probably can tell, I really like concepts that can represent data in different ways and the ability to recover “lost” information due to my prior background in computer science (I studied computer science a while back before coming to CarletonU). To disprove whether or not a transformation is linear is to do the following procedure in this order (because I find this the fastest way to disprove if T is linear or not):
- $T(\overrightarrow{0}) \ne \overrightarrow{0}$ (if $T(\overrightarrow{0}) == \overrightarrow{0}$ then it tells you nothing so you need to go to the next steps)
- Find a counter-example such that for some scalar k and vector v: $T(kv) \ne kT(v)$
- Find a counter-example such that some some vector u, v: $T(u+v) \ne T(u) + T(v)$
One tip when dealing with proving or disproving whether or not T is linear is to assume T is linear and then find that it’s not linear if $T(\overrightarrow{0}) = \overrightarrow{0}$. During the proof, you may notice that there are potential issues with the proof and from there you can try to find a counter-example. Of course, if you can think about a counter-example on top of your head then great but sometimes these types of questions are not intuitive (at least for me).
The topic of linear transformation expands to talking about the kernel and range and their associated size: nullity and rank respectively. Kernel is essentially the nullspace of the linear transformation. It is the set of vectors such that $T(\overrightarrow{0}) = \overrightarrow{0}$ and the nullity is the dimension of the kernel. I always found the name kernel confusing. Hopefully one day I’ll learn why Mathematicians call it the kernel because when I think of a kernel, I think of the core of an operating system (i.e. Linux Kernel). Similar to the nullspace, you can verify your answer by inputting the basis vectors you found when determining the kernel of a linear transformation into the transformation to see whether or not it gives you the 0 vector. The range as the name implies is the output of the transformation which is a subset of the co-domain (I hope you recall this from calculus or Highschool functions course). The size of the basis of the range(T) is called the rank which you should be very familiar with. Finding the range and kernel of a linear transformation is very similar to finding the nullspace and the colspace of a matrix. The similarities between kernel and range with nullspace and colspace are very apparent especially when the rank-nullity is the same for linear transformation but worded differently. Instead of the rank + nullity = the number of columns in the matrix, it’s defined as rank + nullity = dim(V) where V is the domain of the linear transformation.
The next concept relating to linear transformation goes back to my fascination with the Change of Basis vectors. The next concept taught is the matrix representation of a linear transformation. It’s very cool to be able to represent a linear transformation into a matrix. The matrix representation of a linear transformation involves representing a transformation from two different bases similarly to the change of basis matrix. I shall repeat once again, this course is highly interconnected and is built such that the previous concepts are part of the foundation of the building you are building (which in our case is an understanding of linear algebra). The idea of being able to represent some transformation into a matrix is not a new concept, at least not for me. I have learned about rigid body transformation such as rotation matrix (aside: I have a blog post (and animation video which I still need to voice over) about how to use matrix rotation to derive double angles). Anyhow in this unit, you will learn how to find a matrix representation of a linear transformation or how to recover the linear transformation from the matrix (hint: it involves coordinate vectors and a good understanding of how change of basis matrix works).
The next topic still relates to linear transformation and are concepts you should be familiar with from MATH1800 (I had a course transfer from when I took it 6-7 years ago) about whether a linear transformation is injective, surjective, and bijective. Linear transformation from my view is just a function so everything you know about functions applies to linear transformation from what I know. Why is knowing whether or not a transformation is inject or surjective important? It turns out that if a linear transformation is bijective, then the transformation is invertible just like how regular functions work. The idea of bijective gives me encryption vibes whether certain encryption schemes are surjective, injective, or bijective. Though I don’t know much about encryptions unfortunately but that idea popped in my head when learning about this years ago. Anyhow, to figure whether a linear transformation is injective or surjective or both (bijective), it is easiest from looking at the matrix representation and row reducing it. If there are pivots in all the columns after row reducing the matrix, then it is injective and if there are pivots in all the rows, then the transformation is surjective. This should connect the dots that non-singular matrix (matrices that reduce to the identity matrix) are invertible, a neat property that comes from non-singular matrices. To see why having pivots in all the columns or rows in the RREF (Row-Reduced Echelon Form), you should check out the proof which Kyle does provide for anyone interested. I really want to avoid mixing between the course organization and the course content but it’s hard. Anyhow if the linear transformation is not bijective then the linear transformation will not be invertible but it may be left or right invertible. Similarly to how matrices might be left or right invertible (i.e. $M_2M = I$ but $MM_2 \ne I$ or the converse where $M_2$ is some matrix that makes the matrix M left/right invertible). This is why $T(T^{-1}(w)) = v$ but $T^{-1}(T(v)) \ne w$ can occur meaning the transformation does not have an inverse transformation. Talking about invertible matrices, to find the inverse of a linear transformation, it is simply just finding the inverse of the matrix representation and then constructing (i.e. finding the closed form) the linear transformation from the matrix representation.
The course then shifts gears to talk about dot products, norm, unit vectors and orthogonal sets which may or may not be a review. I say everything may or may not be review but to be honest, I only recall their existence but have no clue what they are when I was taking the course. If you are in Physics then you may have seen this before such as in PHYS1001 very briefly. In Physics when dealing with vectors, we need to know whether or not the vectors are orthogonal which is when the dot product between two vectors is equal to 0. In this course, we don’t define the dot product to be $AB\cos\theta$ (recall $\cos 90^\circ = 0$ as we only care about if the two vectors are orthogonal and disregard the vector if they are not orthogonal to each other (i.e. we sum the product between each corresponding entries in the vectors: $u \cdot v = u_1 v_1 + u_2 v_2 + … + u_n v_n$). What confused me about learning about norm is that I always thought the norm meant the perpendicular line. But in this course, it means the distance of the vector from the origin. From this point onwards, the course talks a great deal about the orthogonality of vectors and matrices. As stated earlier, two vectors are orthogonal if their dot products are 0 so by extension, an orthogonal set is simply the set of vectors that are orthogonal. To check if a set is orthogonal, you just perform the dot product on each vector in the set which made me realize an interesting fact. The amount of times you need to perform the dot product is simply ${n \choose 2}$, something you may have encountered in Highschool (I don’t think I did) or in a probability course. But what is interesting about orthogonality? There are a few things but one of the neat properties of orthogonal sets is that an orthogonal set is linearly independent if there is no zero vector in the set for obvious reasons (i.e. the dot product of the zero vector is always zero and is the linear combination of any vector). If an orthogonal set is linearly independent then one could find the linear combination of any vector $w$ belonging to the span of the orthogonal set by simply using some formula to find the coefficient for each basis vector simply by performing two dot products (i.e. $c_i = \frac{w \cdot v_i}{v_i \cdot v_i}$). As Kyle puts it
finding coefficients within an orthogonal basis is faster (dot products, instead of row reducing!
MATH2107 - Lecture 18 - Orthogonal Basis, Complements, and Orthogonal Matrices (Kyle Harvey)
What do we call a set of UNIT vectors that are orthogonal to each other? It is called the ORTHONORMAL SET due to the fact that the vectors are ORTHOgonal and have the norm of 1 (i.e. they are unit vectors). This introduces the idea of orthonormal columns and orthogonal matrices where the property of $U^TU = I$ where U is some matrix that has orthonormal columns (this is a way to verify if you calculated the orthonormal set correctly). This is important to remember when we work with QR factorization and finding the orthogonal projections which we will see later on. The course also introduces Orthogonal complement $W^\perp$ which may be familiar (I did not realize I learned this before till I found my old notes from my transfer credit for MATH1104 the day after I wrote MATH2107 exam). The orthogonal complement is the set of vectors that are perpendicular to everything in some set W. While it may not be apparent why or what this means visually, but everything will make sense in the next topic. Orthogonal projection is the idea of “projecting” (drawing) a vector within some space (plane) or within some vector that is the closest point in the plane or vector to the vector y that is shooting usually outside of the vector or plane. A visual representation would help (which I took without permission as usual):
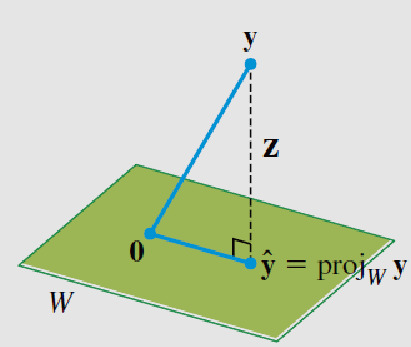
An illustration of a projection over a plane. Taken without permission from the lecture. I'm too lazy to draw one via Manim Library.
From the illustration above, you can see that the projection $proj_w(y) = \hat{y} \in W$ belongs to the plane while the perpendicular line from $\hat{y}$ and the vector $z$ belongs to W complement $W^\perp$. This means that the dot product between $\hat{y}$ and $z$ will be equal to 0 (a way to sanity check your answer). I like to view W complement to be all the vertical lines perpendicular to the surface such that it creates an infinite square (i.e. W is just an infinite surface while $W^\perp$ gives the depth in the cartesian plane). I love visualizing linear algebra which 3Blue1Brown’s Essence of Linear Algebra series and Zach Star’s (you may have remembered him as MajorPrep) application videos do a great job in making linear algebra more intuitive (I really should buy their merch one day to support their works because it’s simply amazing). Anyhow, orthogonal decomposition is simply breaking down the vectors that make up y (i.e. $y = \hat{y} + z$) which is vector algebra you learned in Highschool. Rearranging the equation gives you the ability to find $z \in W^\perp$, the perpendicular line that intersects $\hat{y}$ and the vector y.
What does it mean if z = 0? Does that imply y is in W or not?
The good old Pythagorean theorem comes back since the points: y, $\hat{y}$, and the origin 0 forms a triangle. One way to verify if you calculated either $\hat{y}$ or $z$ correctly is to see if the Pythagorean theorem is violated. If the Pythagorean theorem is violated, then you have calculated either $\hat{y}$ or $z$ incorrectly as they will not be in their respective spanning set. The next topic introduced is still about projections but ties with why we need to learn about orthonormal columns. It turns out we can utilize some property of orthonormal set to find the projected vector $\hat{y}$:
\[\begin{align*} \hat{y} = UU^Ty \end{align*}\]You may have noticed that this course requires a lot of memorization which I dislike. But one neat trick I use to remember the ordering of $U$ and $U^T$ is remembering the fact that when forming a matrix consisting of orthonormal columns, $U^TU = I$ which is likely not what we want or else $\hat{y} = y$ (which is true if $U$ is a square matrix. I should think about this more and email Kyle for an explanation if I cannot wrap my mind on this fact). Another thing you may have noticed that since the topics are so interconnected (i.e. a very dense graph if you get what I am saying), there are so many ways to approach a problem. That is where the course can get very confusing. The next topic is the Gram-Schmidt Process, a keyword I remember learning before but had no recollection how it works. The Gram-Schmidt process is a neat but very annoying process (in my own opinion) to convert any basis into an orthogonal basis. Another topic covered in the course is QR Factorization where a matrix is a QR factorization when $A = QR$ (where Q is a matrix with orthonormal columns and R is an invertible and upper triangular matrix. Although I don’t have a complete picture of QR factorization, it is useful in the next major topic about learning about the least squares method. To calculate R, the following formula is used: $R = Q^TA$. One technique of remembering equations is making a connection to some word, phrase, or idea. A group of students in the class likes to remember transpose as “standing it up” or at least I think that’s what they meant because it’s their inside joke I keep overhearing during lectures. I remember the equation $R = Q^TA$ as “OTA” (over-the-air) update except instead of an “O”, it’s a “Q”. Eventually I forgot the acronym after the test. So for the exam, I simply just derived it (not good if you are crunch in time but luckily I was not):
\[\begin{align*} A &= QR \\ Q^TA &= Q^TQ R & \text{since Q is a matrix of orthonormal columns, $Q^TQ = I$}\\ Q^TA &= IR \\ R &= Q^TA \end{align*}\]You will see again that this is somewhat a common theme I do where I derive the equations because my memory is a goldfish. I just cannot remember anything I learn. This is one of the reasons why I continue blogging because it’s a way for me to quickly recall what I learned. Anyhow, one way to verify if you calculated R correctly is to check if:
- R is an upper-triangular matrix
- QR = A
During the exam (which was 2 days ago at the time of writing this sentence), I calculated R incorrectly despite obtaining an upper-triangular matrix. When I proceeded to verify if QR = A, I quickly found out I matrix multiplied top row incorrectly which was why the check if the matrix is upper-triangular did not catch the error beforehand. Checking your work by utilizing the definitions and theorems is a good way to ensure your answers are correct but do be wary that it might require too much work and time. I just find it as a good method to verify your work because often times it’s hard to pinpoint if your work is correct if you just solved it in the past hour or two. Having a way to verify your solution quickly is very handy (for some reason this reminds me of P and NP where it’s easy to verify the solution to an NP problem in polynomial time but I digress. As you can see, computer science was the gateway for me to be a bit curious about math).
The next topic is an exciting topic for those of you in the sciences because this is the math behind the curve of best fit. You may have learned about the least squares method from PHYS1001 labs, at least the very crude way to calculate the least squares method.
A crude way to find the line of best fit. Taken without permission from the Errors Lab Handout from PHYS1001

Maybe a way to find the least squares. I am not sure but I'm too lazy to read this document. Taken without permission from PHYS1001 Errors Lab Handout
This topic may also be review (I recall learning about it but have no recollection on what it is about till I encountered it again in MATH2107). This unit is very straightforward and the interesting thing about this unit is learning how to find the least squares solution of different polynomials and functions. I only remember learning how to find the least squares line but it turns out that to find the curve of least squares, it’s just an extension to how one would find the least squares line which is very neat. The solution to the least squares is represented as $\hat{x}$ which can be quite a bit of work to find using the usual method (i.e. $A^Tx = A^Tb$). Using the QR factorization learnt in the previous unit, the solution to the least squares can be determined by $\hat{x} = R^-1 Q^Tb$. For the longest time, I had a hard time remembering this so I just derived it whenever I needed it (including the exam but that was to only verify if I remembered it correctly):
\[\begin{align*} A^TA\hat{x} &= A^Tb \\ (A^TA)^{-1}(A^TA)\hat{x} &= (A^TA)^{-1}A^Tb \\ \hat{x} &= ((QR)^T(QR))^{-1}(QR)^Tb \\ &= (R^T(Q^TQ)R)^{-1}R^TQ^Tb & \text{recall Q is a matrix with orthonormal columns meaning $Q^TQ= I$}\\ &= (R^TR)^{-1}R^TQ^Tb \\ &= R^{-1}((R^T)^{-1}R^T)Q^Tb \\ &= R^{-1}Q^Tb \end{align*}\]Of course, you do need to recall a few properties about transpose and inverse, but I find deriving the equations the best way for me to remember and recall the equation due to my very short-term memory. The next major topic is talking about inner products which I find it to be weird. But hopefully, I understand inner products more when I study MATH2152 material after I finish up some tasks I wanted to work on for the remaining days of August or when I take MATH2100 - Algebra. Anyhow, a lot of the properties of dot products such as the work for orthogonality apply to inner products as well. There are three inner products that are covered in the course: $<u, v> = u\bar{v}^T = u\cdot \bar{v}$, $<A, B> = Trace(AB^T)$ and $<f,g> = f(1)g(1) + f(2)g(2) + f(-1)g(-1)$ (though there are various variations to this). Calculating the inner products is EXTREMELY ANNOYING. Attend the lectures and watch the lecture videos for shortcuts on 2/3 types of inner products introduced in the course. It’ll save you TIME!!!!!. After revisiting various things relating to orthogonal sets such as gram schmidt process but for inner products, the last topic talks about symmetric matrices and the Principle of Axis Theorem.
When discussing symmetric matrices, the idea of a diagonalizable matrix shows up once again. Previously it was stated that a matrix is diagonalizable if the matrix can be represented as $A = PDP^{-1}$ where P contains the eigenbasis as columns. However, this time the idea of diagonalization becomes stricter by adding a condition that the eigenbasis must consist of vectors that are orthonormal to each other within the same eigenbasis. This stricter definition of diagonalization is unsurprisingly called the orthogonal diagonalization and is written as $A = UDU^T$ which looks oddly similar to the definition of the diagonalizable matrix: $A = PDP^{-1}$. The direct consequence of this theorem is that for two vectors $v_1$ and $v_2$ belonging to two different eigenbases, $v_1$ and $v_2$ are orthogonal to each other. How orthogonal diagonalization ties in with symmetric matrices (which are matrices that satisfy the property: $A^T= A$ i.e. flipping the rows and columns will still result in the same matrix), is that a matrix is orthogonally diagonalizable if and only if the matrix is symmetric. Showing if a matrix is orthogonally diagonalizable requires a lot of work but verifying a matrix is symmetric is not. This leads to the Spectral Theorem (for Real Matrices as there is the Spectral Theorem for Complex but that is not taught in the course). The spectral theorem (for real matrices) gives some useful properties such as how all the eigenvalues of a symmetric matrix are also real or how A can be represented as a spectral decomposition which I am still trying to wrap my head around why this was introduced. Perhaps because it is part of the Spectral Theorem which has nice properties that can be exploited for the next topic about Quadratic Form and the Principle Axis Theorem.
A quadratic form as the name implies is simply an equation of polynomials that have at most the degree of 2 (i.e. $x^2$). Quadratic form is defined to be the function $Q(x) = x^TAx$ where A is symmetric. An example of a quadratic form is $Q(x) = -3x_1^2 + 9x_1x_2 - 2x_2^2$ (taken from someone’s blog post since I wanted to stop copying examples from the lecture slides and was too lazy to come up with one). Notice the term $9x_1x_2$ are not a polynomial of degree 2 (or not in second order). This term is referred to as the cross-product term which is not desirable which is why the Principal Axis Theorem was introduced. This theorem removes cross-product terms. This relies on utilizing orthogonal diagonalization to reduce the quadratic form to be $Q(x) = y^TDy$. There are two ways how I remember this form. The first being that $Q(x) = x^TAx$ but replacing the variables to be $Q(x) = y^TDy$. The second way I remember this form is by remembering that the Principle Axis Theorem relies on substituting x = Uy into $Q(x) = x^TAx$ which results in $Q(x) = x^TAx$ if you work it out (this is what I did during the exam to verify if I remember this correctly). Quadratic forms can be classified to 5 categories:
- Positive Definite
- Positive Semi-Definite
- Negative Definite
- Negative Semi-Definite
- Indefinite
While I won’t go into too much details, I will briefly cover what positive definite and positive semi-definite means to explain the connection with orthogonal diagonalization and in robotics (a course where I had no clue what I was doing but is the first course along with image processing (that I dropped) where I first learned the applications of linear algebra outside of finding the best line of fit or how Google Page ranking works which I never read but was told about by a professor many years ago. Positive Definite is when $Q(x) > 0 \forall x \ne 0$ while positive semi-definite is when $Q(x) \ge 0 \forall x \ne 0$.
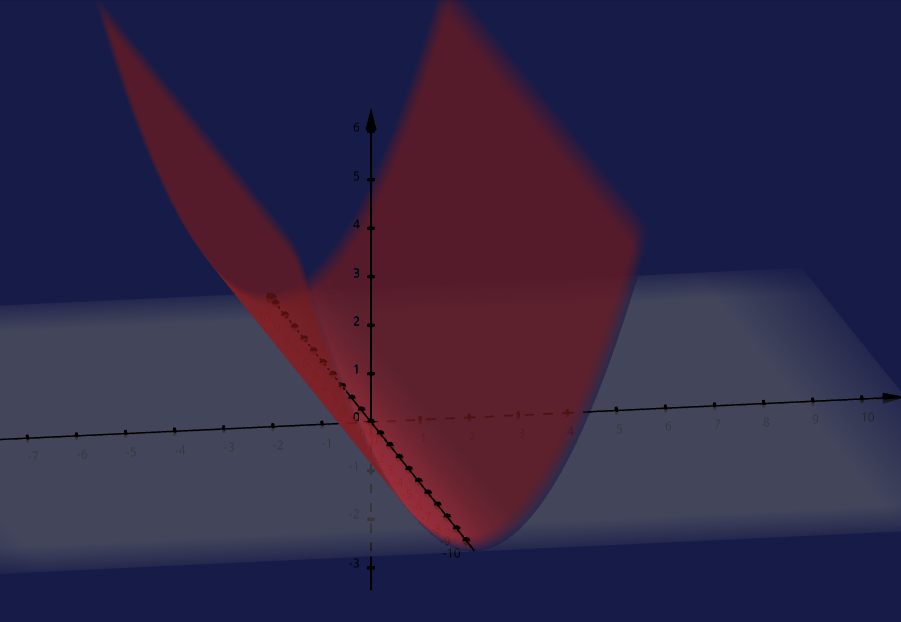
A positive semi-definite quadratic form that I graphed using Geogebra
In the figure above, notice how all values of $Q(x)$ is greater or equal to 0 where the minimum of the graph is 0 even outside of the origin. In contrast, a positive definite is never equal to 0 at any value of x outside of the origin.

A positive definite quadratic form that I graphed using Geogebra
You may be confused as to why we are learning about Quadratic forms. I did not question this before and simply thought it was a nice connection to what we learned about symmetric matrices and orthogonal diagonalization. But it turns out based on some old notes I had from years ago, there is a very important application to this in robotics but I won’t discuss it much (as I don’t remember anything from the course as I was essentially lost in the course) the following block of text from my notes:
A symmetric matrix A is positive definite if its eigenvalues are all positive. One consequence is the condition $x^TAx$ > 0 for all nonzero $x \in \mathbb{R}^n$. Positive-definite matrices have a number of important applications in robotics, for example in evaluating the manipulability of a robot (Chapter 5) and in representing the inertia of a rigid body or a robot (Chapter 8). Since positive-definite matrices are symmetric, they behave like diagonal matrices in the proper choice of coordinate frame.
I definitely should revisit robotics one day and tackle the subject as my math ability has vastly improved since then (though we shall see if MATH2000 and MATH2100 break me inside to not want to touch math ever again). Anyhow, this section of the course review has taken way more time than I initially thought but it was nice to revisit every major topic covered in the course even if it’s only been 2 days since I wrote the exam (hopefully I did well in the course).
Review
Now for the actual course review that you are all waiting for (or not if you skipped the first section). As one would expect, MATH2107 does not have much emphasis on proofs which is either a yay or nay depending on who you ask. As a confession, it was a yay for me despite being in the Math honors program who should be taking the honors version of this course MATH2152. I was originally supposed to take MATH2152 in the winter but an opportunity arose where I got to work at a company specializing in realtime operating systems as a support developer (think of it as being the person who answers StackOverflow questions but to customers). Due to this arrangement and knowing how MATH1152 (Linear Algebra I) was organized, I decided to only take MATH2052 (Calculus and Anaylsis II) due to its asynchronous format (and in which Kyle suggested I take if I only had the option to take only one of them). I also wrote a course review for MATH2052 if you are curious.
MATH2107 is formatted such that the course was a “reverse-style” classroom which made me extremely scared initially due to prior experience with reverse-style classroom. However, Kyle organized the course very well such that the course is very clear and his lecture videos and slides had all the information you needed to succeed in the course. The reverse style classes I took involved an extreme amount of self-studying and agonizing about why your code doesn’t work. For context, I took an introductory to system programming course that was reverse styled where we had to do a series of exercises that were counted to our marks before the lecture. Lectures were for working on problems together with the professor and answering questions that students struggled with on the exercises that we submitted … Anyhow, this is different. It was not anxiety nor frustrating experience I had previously but a very fun experience. I loved taking MATH2107 with Kyle Harvey and I would have to say it is the top 3 courses I’ve taken in terms of enjoyment out of the 47 or so university courses I’ve taken so far (I know I’m old 😅).
Students are expected to have watched the lecture videos before attending lectures (also called the problem-solving tutorial) to work on problems that count as BONUS MARKS (to entice students to come to class). While probably less than half of the class showed up to lectures, the problems we worked on every lecture were very helpful. Every lecture, students are given 6 problems to solve and if the student/group got 3 questions correctly, they are awarded a point. While answering 5/6 questions correctly gives the group 2 points. These points accumulate to a maximum of 40 points throughout the course which gives you a bonus of 2.5% towards your final grade which usually increases a letter grade. Kyle is usually lenient and will still reward you a point provided you were on the right track and generally have the right answer with some small caveats (I think but don’t quote me). You can either work on these problems either by yourself or with others but I just worked on the problem myself as it felt awkward to talk with other students and I also thought to myself that I would learn better if I do these problems myself. Though it would be nice to have a partner with whom you could compare your answers before submitting but I just bothered Kyle instead whenever I had a question or to see if I was on the right track. The reason why lectures are spent practicing problems is that students often do badly in Math because they lack practice. This course requires a lot of practice, especially if you have been relying on an RREF calculator in the previous course due to previous course being online. Linear Algebra is often a hit-or-miss course from seeing the grades of my friend when I took MATH1104 equivalent many years ago. Some of my friends would do way better in calculus compared to Linear Algebra where they bombed the course or do extremely well in Linear Algebra compared to their Calculus marks. I was in the latter where I did alright when I took MATH1104 equivalent (my calculus grades on the other hand … were not great, but at least I did way better than the class average which was a D+). Though I remember nothing after I wrote that exam in my first Linear Algebra course and I didn’t even recognize I learned some of the concepts before when I took MATH2107 till after I wrote the exam when I was looking at my old notes. Shows you how your grades mean nothing if you don’t even recall learning the concept (I understand if you don’t remember the exact details after taking the course but I’m talking about learning the same thing again and not recalling it). One of the greatest things I observed in the lecture is hearing people’s lightbulbs turn on when they finally understand some concept through the guidance of Kyle. This is what reverse-style classroom is supposed to be about or at least in the active learning environment (I do not know my pedagogy terms as you can probably tell). Kyle is experienced at teaching students or at least I think he is based on how he nudges the students towards the answer at the appropriate time. Kyle is open to answering students’ questions and is patient with the students, providing hints and nudging or encouraging the student to figure out the answer which has been effective from my observation. This experience makes me think that reverse learning classrooms doesn’t have to be a frustrating experience. I’ve been told that studies have shown that reverse-style classroom yields better results. But from my observation of reverse style classrooms I’ve taken or observed my juniors taking was that it’s only helpful if the student is willing to put in many many many hours of work. But this is different. Sure this course takes more time than your traditional course because you have to watch the lectures on your own time. But for an extra 3 hours of your own time to get a rewarding experience, it is worth it if you are not taking many courses and not busy like I was during the summer semester (I was only taking PHYS1004 (Introductory Electromagnetism and Wave Motion) and this course so I got plenty of time).
There are twelve assignments in this course delivered through Webwork and only the best 10/12 assignments are counted towards your grade. I simply dropped the last two assignments so that I could focus on my exams so it was nice. While I don’t recall how many questions each assignment has, the first question of every assignment is a True and False question. I believe Kyle chose webwork because it is free as opposed to something like Webassign that I recall using many years ago for my Linear Algebra course that I had to pay a digital access for. Talking about paying for course materials, there is absolutely no need to buy a textbook for this course. Kyle suggested a few textbooks for reference but said in the Syllabus that the course slides will suffice. This is absolutely true. Kyle’s slides are very clear and concise. He organizes his slides very well and places a “strategy slide” whereby he explains how to answer each type of question he will ask on the exam or tests. Kyle did mention to some of us that some students said his slides were concise enough for them that they would not watch the video lectures at all. I do suggest watching the video lectures as it does go more in-depth but if you really insist skipping them, at least watch the video lectures on inner-products because there is a tip that is a time-saver. Another tip is to work on the bonus problems regarding inner product because there is another time-saver technique introduced there. Going back on the topic of the assignments, these are quite time-consuming and a bit frustrating when you cannot solve the question. Each problem has “unlimited attempts” (I think the limit was actually 999 times per question). You are expected to use a matrix calculator such as Symbolab which I heavily used for the assignments, tutorial problems, and bonus problems because some of the matrices will take forever to row reduce. I often resorted to using a spreadsheet program (i.e. Excel for Windows user or Open Office for Linux or Opensource users) to solve the assignments as well. One thing to be careful of is that you cannot leave any input to be blank in each problem or else it’ll report that you got a 0 regardless if all the other answers in the problem was correct. I made that mistake near the end of the course when there was one single question I had absolutely no idea how to do. I personally found the assignment problems to be a painful experience of this course and did not find them useful when studying for the tests. You are better off solving the lesson handouts or the bonus questions covered during lecture. The true and false questions was the most useful thing from the assignment.

An example of how Webwork looks like
There is a tutorial for the course but no one goes from my personal experience as I attended all of them. I would be in the tutorial and there would be at most 2 other students. Sometimes a third student would show up. Since the tutorial attendance was so low, the TA Samik would tell me to go on the board and write my solutions to the tutorial problems so that he can check my work and give feedback on how I should answer the question or if I got the notation incorrectly. For some reason in the course, I got mixed up with not writing the word “span” or mixing up some small nuances in the definition so it was helpful to get my work critiqued. I usually work on the tutorial problems before coming to the tutorials but there were times when I slipped behind and only did half of the problems he wanted to cover for that week. Each lesson (there are two or more lessons per week) has a set of questions broken into three parts. The first part checks if you understood the lecture by asking you definitions or asking you to describe how you would answer a certain type of question. The second part is practicing the concepts through a series of exercises. The last part of the lesson questions (which is titled homework) is the thinking question which is geared toward those who want to do Honors level Math. These problems can be quite interesting so I would try to answer the questions and see how far I can go before I give into temptation and read the solutions. One of the greatest things about proofs is that it helps you understand the concept better by understanding how or why a particular theorem, lemma, corollary, or formula works. Sometimes I get curious as to why some theory is true so I would check the proofs that Kyle provides on Brightspace for anyone curious. Talking about thinking questions, Kyle typically puts a thinking question at the end of every bonus lecture problem (Question 6) where students need to think deeper as it’s not obvious and is to give students a small taste of what honors math is like. I deeply appreciate the fact he tries to introduce bits of theory/thinking questions for those interested in Honors Math because the problems he selects are not overwhelming that students cannot figure out (and Kyle was always there to provide hints whenever you get stuck). I did have prior exposure learning math from Kyle as he holds the PSS (Problem Solving Sessions for Math Honors students) online so I knew beforehand that he can teach well. One interesting thing from my memories of the PSS is how he would introduce topics during the session which foreshadows some of the concepts covered in this course. Just a side tangent I wanted to mention.
In terms of office hours, almost no one attends office hours that Kyle holds which is somewhat surprising (not really since it is summer). That just means I get to hog his time to ask questions about the course and even materials outside of the course or just go on random tangents talking about programming, how the university works and stories we have to share whenever I feel like talking to him. I often spent my time in the MTC (Math Tutorial Center) where Kyle holds his office hours in the summer since I cannot find myself to study at home. I get too distracted at home so the bulk of my studying and work is done at that room. Talking to Kyle was oddly very easy which was somewhat weird because I find it very hard to talk to my classmates these days (I am a loner except via Discord or emails which I am quite active).
The course has three tests and only the best two out of the three tests are counted. For some odd reasons, there were a good number of students who skipped the first test which was the easiest test. But I guess that means students will have to do the next two tests. I attempted all three tests as it was good practice for the exam and I didn’t score as well as I wanted to on the second test (I got a good mark but I wanted a higher mark because the exam was worth 50%). The tests pulled no surprises at all and every single question should have been clear to the students if they attended the bonus lecture problem sessions or read over the lecture slides. The tests were very straightforward is all I can say and the same applies to the exam. The exam gave me anxiety as I rarely wrote an exam worth more than 40% in the 47 courses I have taken. This may seem odd but I think a lot of my professors and the departments at the school I went to really hated the idea of having an exam that determined 50% of your grades. I absolutely hated the idea of the exam being worth so much but apparently that was the standard exam weight at the Math department at CarletonU so nothing I can do about that. I pretty much gave up studying for my physics exam (well I didn’t like the course much compared to math so I wouldn’t have studied much anyways even if the physics exam was worth more) and focused on studying math as it was the day after each other. The exam was not as bad as I expected despite studying less than I wanted (it was hard getting myself to study when I just wanted to play with all the distractions around me at my room). I did feel like I knew my material but just lacked practice so I was fairly calm when the day of the exam came. I got less nervous about the exam the more I prepped which is how it should be anyways. Hopefully I did well on the exam but I shall see when the marks comes out. I am hoping for a certain mark which I won’t disclose for now but I somehow doubt I would get it since I always make a small mistake or don’t answer the question in a manner that pleases the professor. The interesting thing about Linear Algebra as I stated in the previous section was how interconnected the ideas were and that there were many ways to verify if your solution is correct or at least in the right direction which I utilized during the last hour of the exam after I went to a quick washroom break as I was finished with the exam after two hours. It was a good thing I went over my work on the last hour because I found a few mistakes on the test when I went to verify a few of the questions such as finding the the upper triangular matrix R as I described in the previous section. When I said I was fairly calm as the exam came closer, I actually was day dreaming during the exam thinking about some anime for a good while which makes me worried if I did well on the exam but what can I do about it now that I submitted the exam. The exam was in-person so it was nice to have MATH2107 be my first in-person exam in a long time as I expect all my exams to be in-person from now on after being spoiled with online exams where I can reference my cheat sheet that I wrote specifically for the tests and exams in the fall and winter since they were open-book.
I believe taking MATH2107 has taught me linear algebra more than what MATH2152 could have provided me (something I need to review before the fall semester starts) simply because I enjoyed talking with Kyle and the difficulty of the course wasn’t big which allowed me to dig into the course materials without trying to play catch-up all the time. The difficulty was just right for me to explore what I wanted in the course without being boggled down with mind-breaking proofs that would make me stuck for hours or days to solve the problem. Though I probably should have attempted every proof for which Kyle provided the proof but I am not that diligent of a student to go through every single proof. I just select which proofs I was interested in, think about it for a few minutes and then look at the proof itself. I probably could have handled more challenges than what I encountered in the course as I am a bit more experienced as a student. In this course, I believe anyone can do well if they put in the work as opposed to honors math where I think it’s a hit or miss depending on the individual if putting in more work will lead to getting a good mark. I am not saying putting more work in honors math doesn’t give you the returns but I think the return is much smaller than a regular math course such as MATH2107. I’ve seen many students who put in a lot of work in courses (from any department) including myself when I was studying Computer Science but their grades were not as good as one would expect from the amount of effort they put in. This made me realize students learn at very different paces which isn’t too surprising. Sometimes students need time to familiarize the concepts and be exposed to different subjects and ideas before revisiting something they once struggled with. I personally was not good at math (I still am not) but my exposure to math and computer science makes me think I can now tackle math (not sure about physics though …). A professor I had for various courses always emphasized at the beginning of the semester that the key to success is to be interested. While it may be hard to be interested (sorry physics), I find this often true for myself. I usually do relatively well in courses that interest me regardless of difficulty. This makes a lot of sense because you are frequently thinking about what you learned throughout the day at random times.

Be Interested is what one of my favorite professor Larry Yulei Zhang who is now at YorkU often said to the class
Anyhow, I am glad I took MATH2107 with Kyle. It does make me sad that I probably won’t be taking another course that is taught by Kyle due to my program requiring a lot of other courses in Math and Physic. Though I am extremely tempted to downgrade Physics to a minor and probably will so maybe I can make space to take another course that is taught by Kyle or perhaps take Linear Programming if Kyle teaches it next summer and I happen to be working in Ottawa during the summer.
How I Took Notes
I am going to be open with the fact that the way I study is very inefficient. I spent countless of hours in most of my courses studying but yields very little returns compare to my peers who study way less than I did. It does probably have to do with different in the speed of learning but it is also the way we approach studying as well. But I thought I would share how I study (this is probably the first course review I have done so) because I tried something new which I found was helpful. Traditionally since Highschool, I would always rewrite my notes to force myself to go over the course lectures.

How my course notes typically look like
This process consumes a ton of time and it’s also a pain to write relatively straight as well. Which is why I am going to switch back to line paper despite how much I hate looking at line paper (there’s just too many lines). If the course offers slides that are good as Kyle’s, I suggest just reading off the slides instead of writing notes that are exactly identical to the lecture slides. Being the idiot I am, I may still continue writing course notes even if the slides are good due to it being a habit.
Cue Cards: Kyle has long suggested to me to try cue cards ever since I knew him from the Problem Solving Session back in the Fall semester. I decided to try it out but not in the manner he would have hoped I use it for. The way Kyle approaches to cue cards reminds me of how Anki works where it is based on repetitive learning (though Anki goes the extra step and does spaced repetitive learning) where you look at the cue cards that you struggle the most more frequently than the cue cards you can solve very easily. I did not do that at all. Similarly to my lecture notes, I handwritten the course notes into different cue cards … which is probably not ideal.

Cue cards I made for MATH2107 as an experiment on its effectiveness. A teddy bear for scale.
As you can notice, I split the deck of cue cards into two categories, one is theory (colored in pink or yellow) and the other are problems covered in the lecture (in blue or turquoise). There are four groups in each category corresponding to how the course was split. There were 3 tests so the first 3 decks in each category corresponded to each individual test while the last deck of cue cards covered the remaining material in the course that the tests did not cover. What was great about cue cards even if I did not use them in the way Kyle or others may have use their cue cards is that I can randomly sort the cue cards and test myself which my course notes do not offer as they cover the course material in sequential order. As for the cue cards that cover the lecture problems, I do not actually solve them but rather think of how I would answer them by either mentally or on a scratch paper the steps to answer the question with the formulas and matrix if applicable written down.
Overall my experience with cue cards have been positive but the downside is that it consumes a lot of time to write cue cards. I do not think I will be using cue cards for my future courses aside from maybe writing the definitions and theorems because it wouldn’t be feasible to write cue cards when I am taking a full course load.
As for how I studied in the course, I did the following:
- Attempted most or all the weekly practice problems every week
- attended office hours to ask questions to either the TA or to Kyle
- rewrite course notes
- write cue cards and test myself the day or two before the test if I had the general idea on how to approach the problem or knew my theory
- try all the lecture bonus problems relating to the test
- read over my course notes at least once before the test
- avoid studying from the assignment questions, those questions are either long or difficult to be on the test
Note: The reviews are bias and reflects my perception of the course. In addition, the information varies depending on the professor and will likely be outdated.
For More Bias Course Reviews:
- MATH3001 - Real Analysis 1
- MATH1800 - Introduction to Mathematical Reasoning
- MATH2000 - Multivariable Calculus and Fundamentals of Analysis [Fall+Winter]
- PHYS1004 - A Review on Introductory Electromagnetism and Wave Motion
- MATH2107 - Linear Algebra II
- MATH2052 - Calculus and Introductory Analysis II
- PHYS1001 - A Review on Foundations of Physics 1
- MATH1152 - Introductory Algebra 1
- MATH1052 - Calculus and Introductory Analysis 1
- Bias UTM CS Course Review