Common Mistake - Divide by 0 unknownly

Math has a lot of rules and hidden intricacies. From elementary or middle schools, students are taught not to ever divide by 0. While most students take this to heart, a common mistake students make is dividing by some function or variable that can be 0 in its domain. This error is not unique to students learning Math but also made by beginners in programming.

For instance, a Highschool student may be asked to create a simple calculator where one of the operations is a division and forget to check if the operation is valid before performing the operation.

Code:

#include <stdio.h>
#include <stdlib.h>

int main () {
	int num1, num2;
	printf("First number: ");
	scanf("%d", &num1);
	printf("Second number: ");
	scanf("%d", &num2);
	printf("%d / %d = %d", num1, num2, num1/num2);
}

Result:

$ ./a.out 
First number: 1
Second number: 0
Floating point exception (core dumped)

I recently got the opportunity to be a teaching assistant for a calculus course for engineers. It came to my attention when marking their assignments a common mistake whereby students were dividing by 0. Unlike the common mistakes non-engineers and Highschooler makes whereby they divide by 0 without restricting the domain (i.e. state $x \ne 0$), this was a bit more interesting. While I cannot provide the exact question due to academic intellectual property reasons, here is a similar problem:

Solve for x: $\sin x + \sqrt{2}\cos x \sin x = 0$ for $0 \le x \le 2\pi$

To approach the problem, some students may do the following:

However, this is a division by 0 error. As to why this is a division by 0, one needs to recall the graph of $\sin x$:

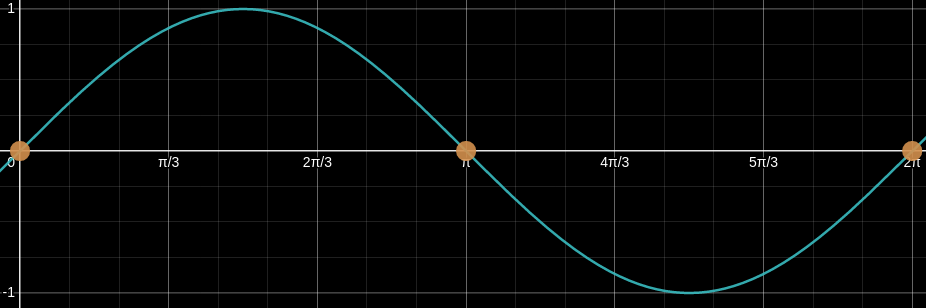
$\sin x$ can be 0 when $x = 0, \pi, 2\pi \in [0, 2\pi]$ where the domain is specifically mentioned in the question. Dividing by $\sin x$ on both sides is illegal and will omit the possible values x could be.

This was interesting because it’s a division by zero through a trigonometric function and not some polynomials that I am used to seeing students including myself make. It never occurred to me how sneaky trigonometric functions and functions in general can be.

Note: It is unlikely I will be writing any technical blogs till February since I have not gotten much time to fiddle with computer science and programming for a while.